이전 글에서 장외채권을 구매하는 법, 채권가격과 금리와의 관계에 대해서 알아보았는데요. 이번 글에서는 채권의 듀레이션에 대해서 이야기 해보겠습니다. 채권 듀레이션 개념을 이해한다면, 자신이 보유한 채권의 금리 리스크를 측정하는 데 사용할 수 있고, 무엇보다 시장 상황에 따라서 듀레이션이 다른 채권으로 스위칭하는 전략으로 활용할 수가 있습니다.
예를 들어 금리 인상이 예상이 된다면, 듀레이션이 짧은 채권으로 스위칭하거나 듀레이션이 긴 채권의 인버스 상품을 사는 방식으로 활용할 수 있습니다. 듀레이션 개념을 먼저 살펴볼께요.
채권 듀레이션 개념
채권을 공부하다 보면 자주 등장하는 개념이 듀레이션입니다. 사전적인 의미로 Duration 은 기간 또는 만기라는 뜻이고, 채권의 Duration은 채권 현금흐름의 가중평균만기라는 의미로 많이 쓰입니다. 그러니까 이자나 원금을 현금흐름으로 보고 이 현금흐름의 평균만기를 구한 것인데요.
채권의 듀레이션 즉, 현금흐름의 가중평균만기가 길수록 금리 변화에 따라 채권 가격 변동이 커져서 듀레이션을 금리 변화에 대한 민감도라기도 합니다. 간단한 예를 들어 보겠습니다.
채권은 자금을 빌려주고 받는 권리 증서입니다. 예를 들어 친구한테 1000만원을 빌려줬다고 가정해봅시다. 친구는 2년 후에 1000만원을 갚기로 했습니다. 2년이 지난 후에 친구가 1000만원을 갚았다면 이 채권의 현금회수기간은 2년이 되겠죠?
바로 이 2년이 바로 이 채권의 듀레이션입니다.
반면에 1년마다 500만원씩 갚기로 했다면, 친구는 1년차에 500만원 2년차에 500만원을 갚아 2년만에 돈을 다 갚게 됩니다. 이때의 현금 회수 기간은 가중평균개념을 써서 1.5년이 됩니다. ((1년x500만 + 2년x500만원) / 1000만원) 이 채권의 듀레이션은 1.5년이 되겠네요.
위의 예시들은 현금흐름의 현재가치를 고려하지 않은 것이라 실제 듀레이션 계산방법과는 약간 다르지만 듀레이션이 현금흐름의 가중평균만기라는 개념만 잡으셔도 충분합니다.
채권 듀레이션 계산
듀레이션 계산방법에는 몇가지가 있지만 보통 1938년 프레드릭 맥클레이(Frederic Macaulay)가 개발한 맥클레이 듀레이션을 사용합니다.
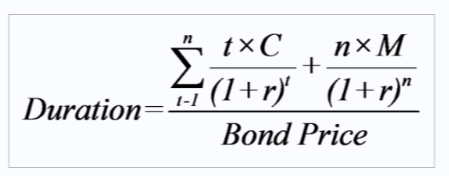
- M : 액면가 (Par value)
- C : 이자 (Coupon)
- r : 채권만기수익률 (Yeild to maturity)
- t : 현금흐름 발생시점 (Year)
- n : 현금흐름 발생횟수
- Bond Price : 채권가격 (현금흐름을 채권만기수익률로 할인한 값)
예를 들어 보겠습니다. 액면가가 10,000원인 채권이고, 표면금리는 8%, 만기3년, 이자는 연1회 지급하는 채권입니다. 채권만기수익률은 10%로 보겠습니다.
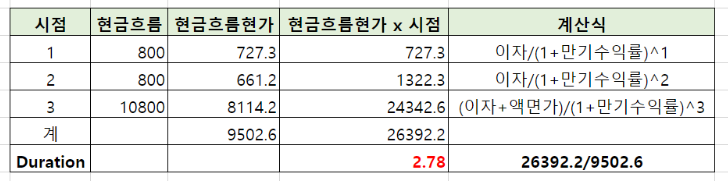
위 계산식에 따라서 현금흐름현가X시점을 현금흐름현가(채권가격이죠?)로 나눴더니 2.78이 나왔습니다. 바로 저 2.78이 이 채권의 듀레이션입니다.
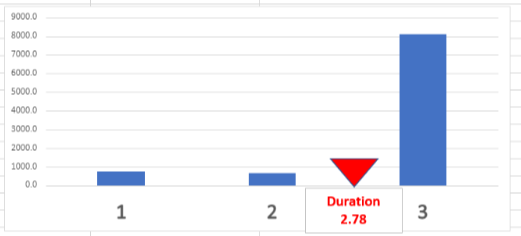
그래프로 보면 듀레이션의 의미를 명확히 알 수 있습니다. 1년, 2년, 3년차의 현금흐름이 있고 듀레이션은 현금흐름의 가중평균을 의미하므로 그 평균이 현금흐름의 사이 어딘가에 오는 것을 알 수 있습니다. 위 예제에서는 3년차의 현금흐름이 큼으로 듀레이션이 3년에 쏠려 있는 것을 알 수 있습니다.
채권 듀레이션의 속성
위 계산식을 통해서 채권의 듀레이션 속성에 대해 알아보겠습니다.
- 채권의 만기가 길어질수록 듀레이션은 증가한다. (중심점이 오른쪽으로 이동)
- 채권의 만기 수익률이 증가할수록 듀레이션은 감소한다. (중심점이 왼쪽으로 이동)
- 채권의 표면금리가 증가할수록 듀레이션은 감소한다.
- 이자 지급빈도가 증가할수록 듀레이션은 감소한다.
- 무이표채의 듀레이션은 만기와 동일하다.
- 이표채의 듀레이션은 항상 만기보다 작다.
채권 듀레이션의 이용
듀레이션의 계산 방법을 아는 것보다 개념을 이해하고 이를 이용하는게 더 중요하다고 할 수 있습니다. 듀레이션의 유용성은 주로 채권의 금리 민감도를 측정하여 금리변동에 따른 리스크를 관리하는 수단으로 활용가능합니다.
예를 들어,
- 금리 상승의 위험을 줄이려면 (기준 금리 상승에 따라 채권 가격이 떨어지므로..) 듀레이션이 짧은 채권으로 포트폴리오를 구성하고,
- 금리 하락이 예상되고 이를 적극적으로 활용하겠다고 하면, 듀레이션이 긴 채권으로 포트폴리오를 구성합니다. (금리 하락에 따라 듀레이션이 긴 채권들의 가격이 더 급하게 상승하겠죠?)
올해 초 미연준에서는 인플레이션을 잡을 때까지 여러차례의 자이언트 스텝을 하겠다고 발표했었습니다. 그 상황에서는 포트폴리오의 장기 듀레이션 채권을 줄일 필요가 있었습니다. 불필요한 리스크는 줄이고 가는 게 좋았었습니다. 반면에 내년부터 금리 인하 및 동결이 예상되는 상황이라면 포트폴리오에서 장기 듀레이션 채권 비중을 늘리는 것으로 대응할 수 있습니다.
그럼 마지막으로 듀레이션에 따른 채권 가격 변동을 극명하게 비교하기 위해서 대표적인 미국 장기채인 TLT와 단기채인 SHY의 가격을 가져왔습니다.
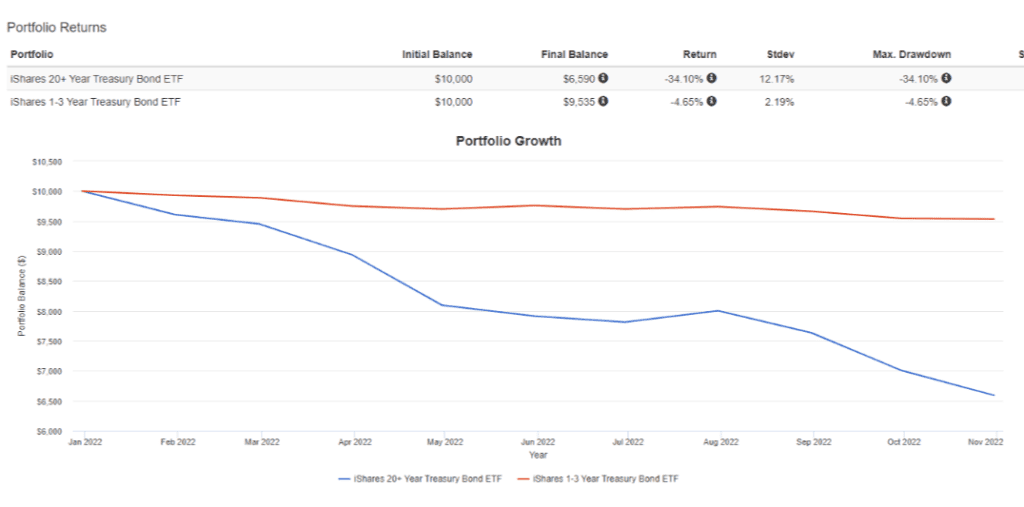
금리 상승의 직격탄을 맞고 TLT는 연초 대비 -34% 하락한 반면에 SHY는 -4.6% 하락에 그쳤습니다. 금리 상승 및 인하는 누구도 예측할 수 없지만, 올해와 같이 대놓고 금리 인상한다는 상황이라면 리스크 관리 차원에서 포트폴리오 조정은 필수입니다.
인플레이션 상황과 미연준 발표를 보면서 잘 대응하시길 빕니다~!!
마지막으로 금리 인상이 정점에 오르고 금리 인하가 예상된다면? 오늘 배운 지식을 응용해서 듀레이션이 긴 채권에 투자를 해야겠죠? 금리 인하시에 채권 가격이 더 높이 오를테니까 말이죠.
아래 미국 장기채 ETF와 한국 장기채 ETF를 소개해 드릴테니 투자에 참고하시기 바랍니다.


